これまでパスワード管理していた教材も,すべてアクセスフリーにしました。ご活用ください。
投稿者: knishimura
『交通事故を減らそう』のJavaバージョンを公開しました。
ブラウザのFlashアプリに対するセキュリティの強化等によりご不便をおかけしていましたが,このたびJavaバージョンが完成しました。もちろん,日本語版で,動きも軽快です。ぜひご活用ください。
組織のページを更新しました。
はじめてBowlandMathsの教材で授業しようとする先生向けに,スターターキットを作成しました。
エイリアン(予定)
Coming soon…
こちらのスターターキットは近日公開予定です。
スピードカメラ
「スピードカメラは交通事故の原因となっているかもしれない」という報道の真偽を,乱数シミュレーションを活用しながら検討する。
確率の理解を深め,不確実な事象において確率に基づいて判断する力を育成します。
授業ガイド
 課題
課題
スピードカメラを設置した800カ所のうち70カ所で交通事故が設置前より増加したと新聞記事は報じている。あなたはこの記事に賛成か反対か。……
詳しくは、PDFをダウンロードしてください。
評価のルーブリック
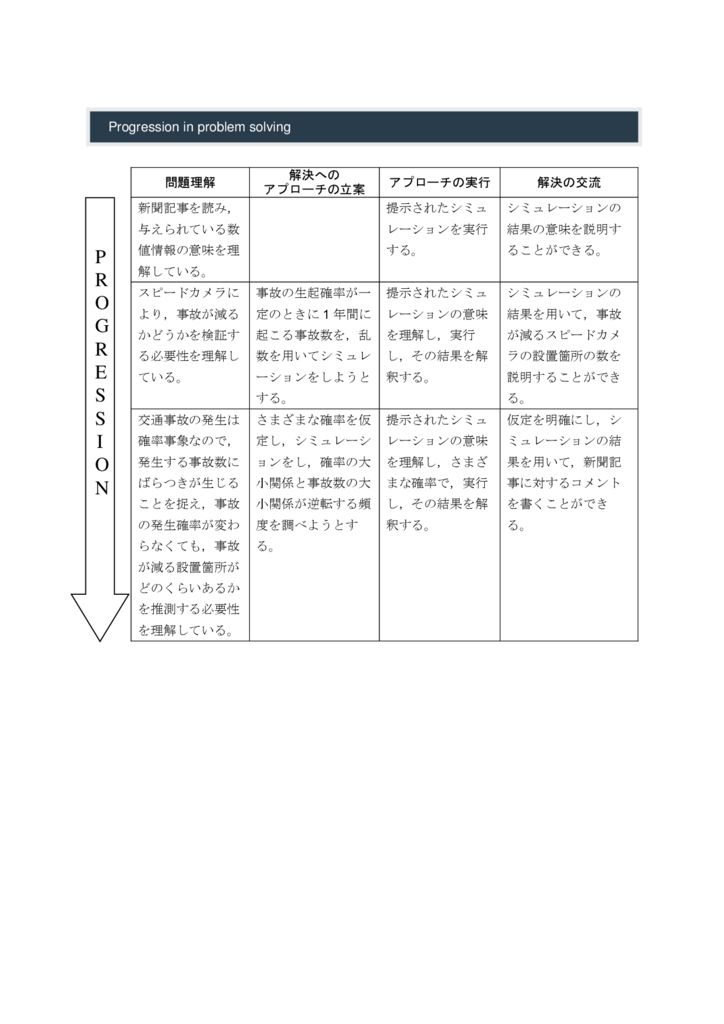 1.問題理解:新聞記事を読み,与えられている数値情報の意味を理解している。→解決へのアプローチの立案:提示されたシミュレーションを実行する。→アプローチの実行→解決の交流:シミュレーションの結果の意味を説明することができる。……
1.問題理解:新聞記事を読み,与えられている数値情報の意味を理解している。→解決へのアプローチの立案:提示されたシミュレーションを実行する。→アプローチの実行→解決の交流:シミュレーションの結果の意味を説明することができる。……
詳しくは、PDFをダウンロードしてください。
ダウンロード
スプレッドシート
新聞記事
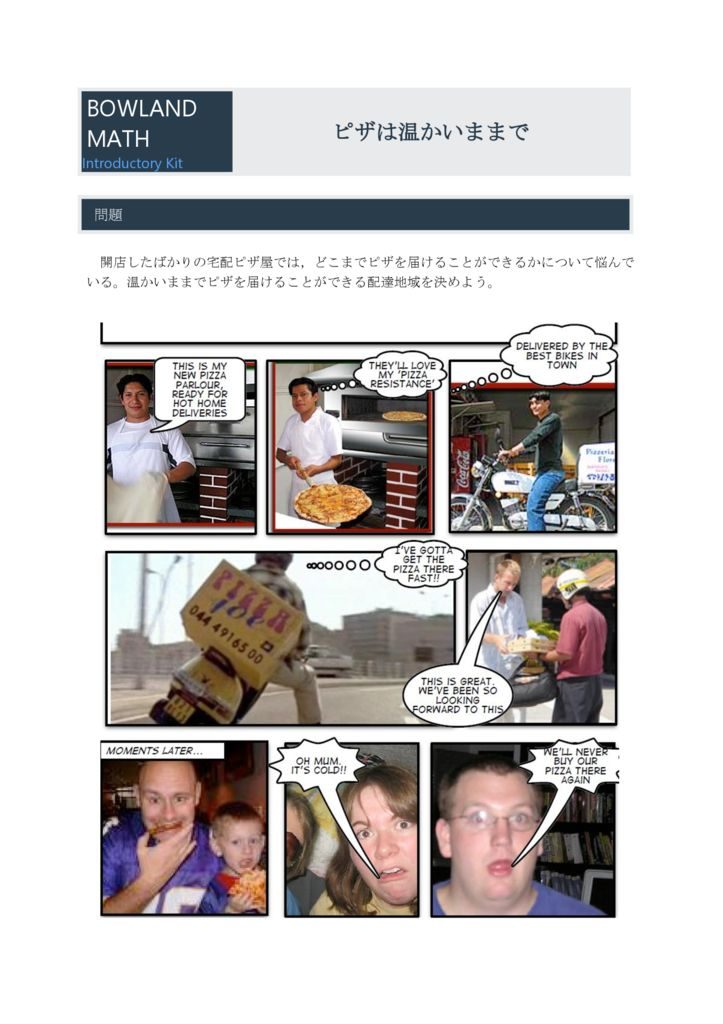
ピザは温かいままで
宅配ピザのパッケージの保温効果を調べ,温かいピザを届けることができる配達地域を決めます。
関数関係があるとみなし数学的に考察したり,得られた結果を解釈したりする力を育成します。
授業ガイド
 問題
問題
開店したばかりの宅配ピザ屋では,どこまでピザを届けることができるかについて悩んでいる。温かいままでピザを届けることができる配達地域を決めよう。…
詳しくは、PDFをダウンロードしてください。
評価のルーブリック
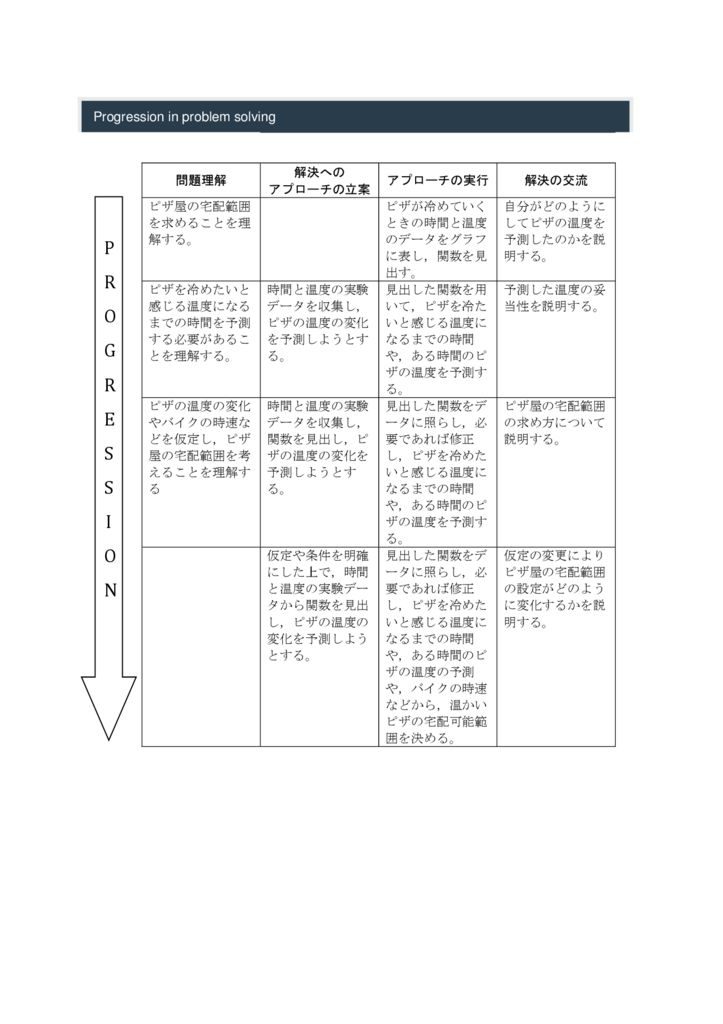 1.問題理解:ピザ屋の宅配範囲を求めること理解する。→解決へのアプローチの立案→アプローチの実行:ピザが冷めていくときの時間温度のデータをグラフに表し ,関数を見 出す。→解決の交流:自分がどのようにしてピザの温度を予測したのかを説明する。…
1.問題理解:ピザ屋の宅配範囲を求めること理解する。→解決へのアプローチの立案→アプローチの実行:ピザが冷めていくときの時間温度のデータをグラフに表し ,関数を見 出す。→解決の交流:自分がどのようにしてピザの温度を予測したのかを説明する。…
詳しくは、PDFをダウンロードしてください。
ダウンロード
ピザが冷めていくときの時間と温度のデータ
データ収集方法の説明ビデオクリップ
データ収集方法の様子
ピザを冷たいと感じる温度の実験ビデオクリップ
グラフから式をつくることができるソフトウェア
アウトブレイク
ウィルス感染による病気拡大を阻止する科学者となり,感染者の発見につながる戦略を考え,ワクチンを開発し,ウィルスの拡大を最小限に抑えるためのワクチン接種計画をつくります。
社会的な事象に対して仮定を設定し問題解決をし,その妥当性について議論する力を育成します。小学生から高校生まで幅広くご利用いただけます。
授業ガイド
ある町で病気が蔓延している。あなたはワクチン接種を任されている。平等に,次の2つのワクチンの使い方を管理する必要がある。あなたは,どのようにすれば最も効果的に……
詳しくは、PDFをダウンロードしてください。
評価のルーブリック
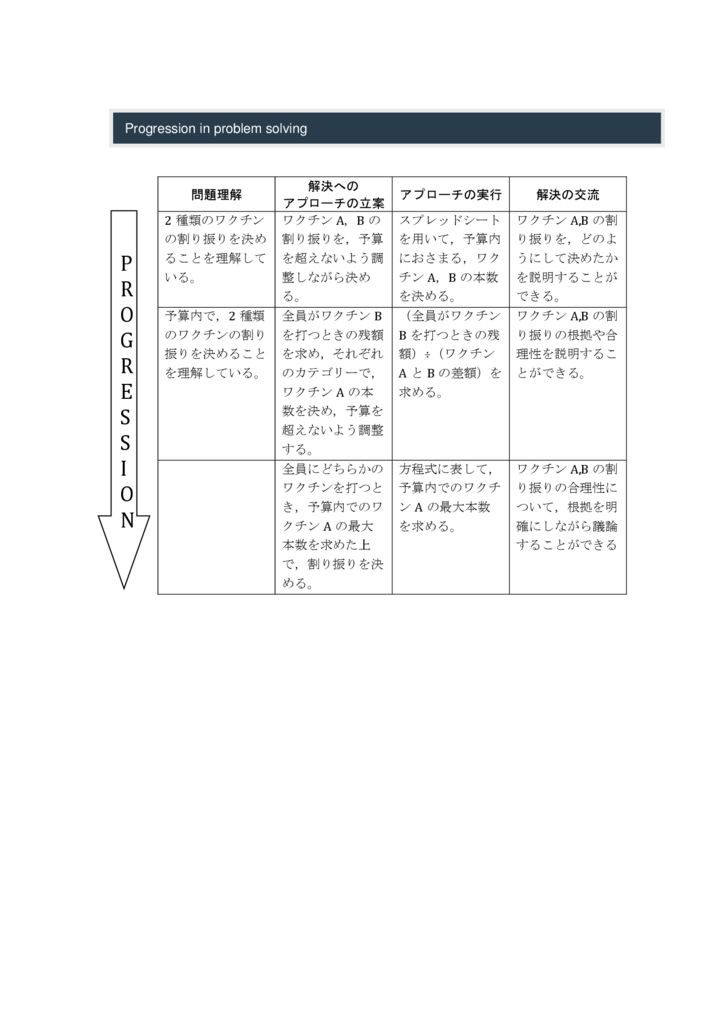 1.問題理解:2種類のワクチン の割り振を決めること を理解して いる。→2.解決へのアプローチの立案:ワクチン A,Bの 割り振を,予算を超えないよう調整しながら決める。→3.アプローチの実行:スプレッドシートを用いて,予算内におさまる,ワクチン A,Bの本数 を決める。→4.解決の交流:ワクチン A,Bの割 り振を,どのようにして決めたかを説明することができる。…
1.問題理解:2種類のワクチン の割り振を決めること を理解して いる。→2.解決へのアプローチの立案:ワクチン A,Bの 割り振を,予算を超えないよう調整しながら決める。→3.アプローチの実行:スプレッドシートを用いて,予算内におさまる,ワクチン A,Bの本数 を決める。→4.解決の交流:ワクチン A,Bの割 り振を,どのようにして決めたかを説明することができる。…
詳しくは、PDFをダウンロードしてください。
交通事故を減らそう
交通事故が多発して困っている町の過去 4年間の交通事故のデータを分析し,どこにどのような対策を講じればよいかを考え,町議会に提出する対策プランを作成します。
ソフトウェアを用いてデータを分析することを通して,統計的問題解決力を育成します。小学生から高校生まで幅広くご利用いただけます。
授業ガイド
 問題
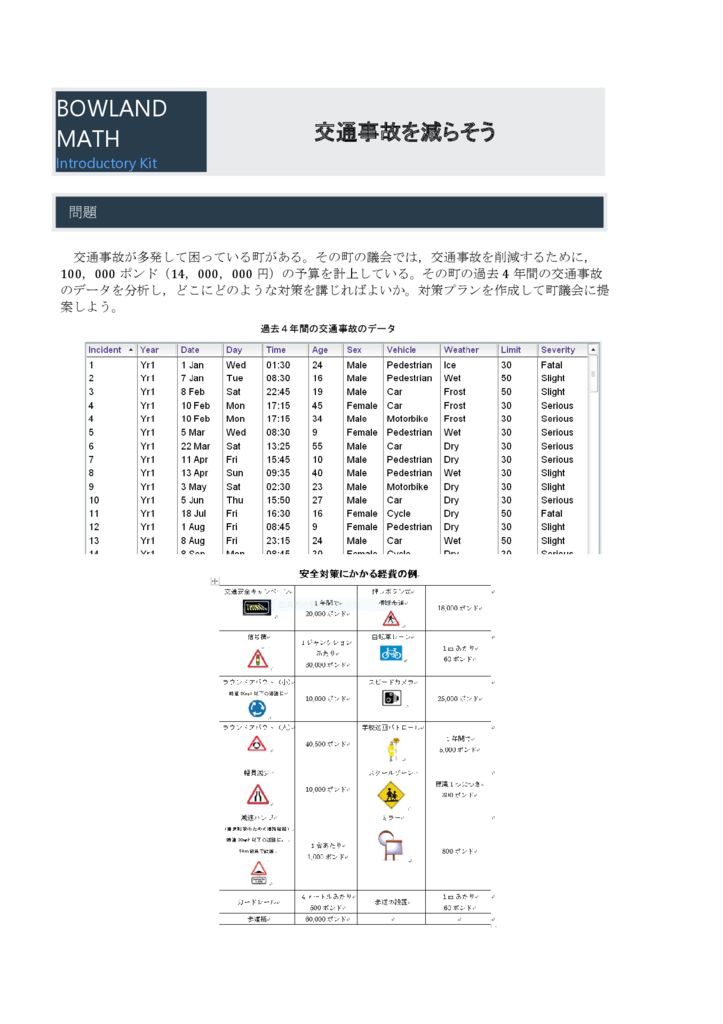
問題
交通事故が多発して困っている町がある。その町の議会では,交通事故を削減するために,100,000ポンド(14,000,000円)の予算を計上している。その町の過去4年間の交通事故のデータを分析し,どこにどのような対策を講じればよいか。対策プランを作成して町議会に提案しよう…
詳しくは、PDFをダウンロードしてください。
評価のルーブリック
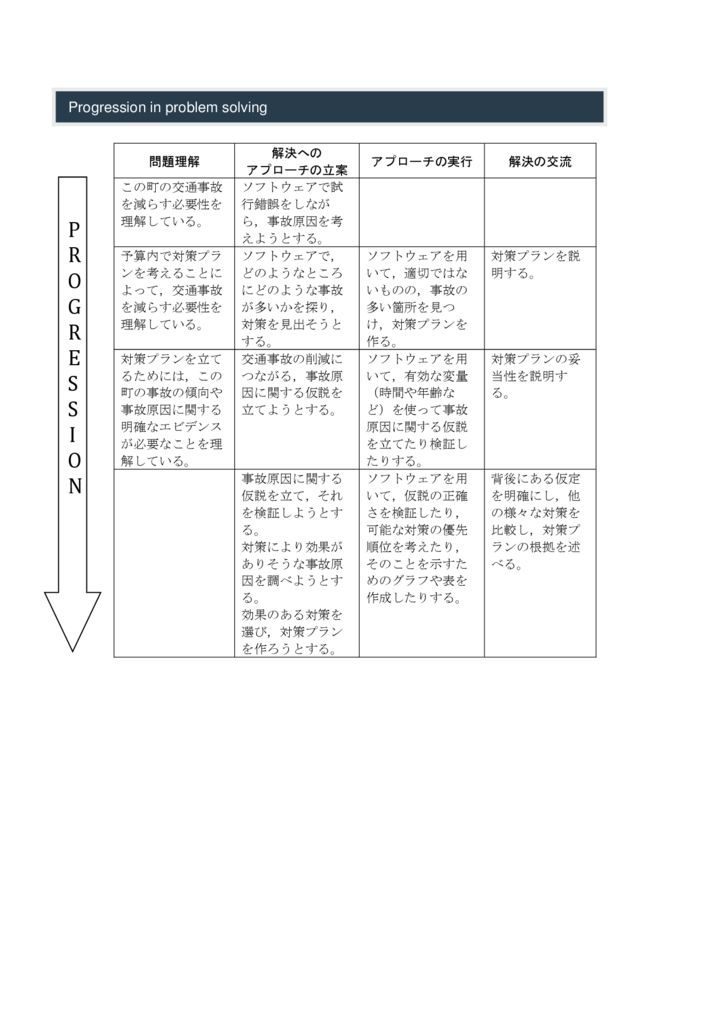 1.問題理解:この町交通事故を減らす必要性を理解している。→解決へのアプローチの立案:ソフトウェアで試行錯誤をしながら,事故原因を考えようとする→アプローチの実行→解決の交流 / 2.問題理解:予算内で対策プランを考えることによって,交通事故を減らす必要性を理解している。→アプローチの立案:ソフトウェアで,どのようなところにどのような事故が多いかを探り,対策を見出そうとする。→アプローチの実行:ソフトウェアを用いて,適切ではないもの,事故の多い箇所を見つけ,対策プランを作る。→解決の交流:対策プランを説明する。…
1.問題理解:この町交通事故を減らす必要性を理解している。→解決へのアプローチの立案:ソフトウェアで試行錯誤をしながら,事故原因を考えようとする→アプローチの実行→解決の交流 / 2.問題理解:予算内で対策プランを考えることによって,交通事故を減らす必要性を理解している。→アプローチの立案:ソフトウェアで,どのようなところにどのような事故が多いかを探り,対策を見出そうとする。→アプローチの実行:ソフトウェアを用いて,適切ではないもの,事故の多い箇所を見つけ,対策プランを作る。→解決の交流:対策プランを説明する。…
詳しくは、PDFをダウンロードしてください。
[訃報]Bowland Mathsに深く関与され,来日もしていただいたMalcom Swan先生(University of Nottingham)がかねてより病気療養中の処薬石効なく4月24日ご逝去されました。遠く日本の地からご冥福をお祈りいたします。来日時の講演録を掲載します。
『真の問題解決能力を育てる算数授業』『真の問題解決能力を育てる数学授業』を明治図書より出版しました。
『真の問題解決能力を育てる算数授業』,『真の問題解決能力を育てる数学授業』を明治図書より出版しました。
今回の学習指導要領の改訂に際しては,小・中・高等学校教育を通じて育成を目指す資質・能力を「知識・技能」「思考力・判断力・表現力等」「学びに向かう力・人間性等」の三つの柱に沿って明確化し、各学校段階を通じて、実社会との関わりを意識した数学的活動の充実等を図っていくことが強調されています。また,これまで学校での学びを中心に展開してきた算数・数学の学びについて、地域社会等の活力を生かし、児童生徒の数学的に考える資質・能力をより確かで豊かに育成していくことも要請されています。このような資質・能力は具体的にどのようなことで,どのように育成・伸長を図るかについての一つの案を提示しました。
『数理的意思決定力の育成に関する ホリスティック・アプローチ研究』の研究成果報告書が完成しました。
平成25年度~平成27年度科学研究費補助金基盤研究(B)『数理的意思決定力の育成に関する ホリスティック・アプローチ研究』の研究成果報告書が完成しました。こちらからダウンロードできます。
BowlandMaths.の主要教材をダウンロード可能にしました。
パスワード設定も解除しました。
各教材のページで,「ダウンロード」タグをクリックしてください。
感想をお聞かせいただけますと幸いです。
『数理的意思決定力の育成に関するホリスティック・アプローチ研究』のwebページを立ち上げました。
『数理的意思決定力の育成に関するホリスティック・アプローチ研究』のwebページはこちらです。
大阪府の中学校の野村太郎先生より,「ピザは温かいままで」の授業記録をお送りいただきました。
大阪府の中学校の野村太郎先生より,「ピザは温かいままで」の授業記録をお送りいただきました。詳細は下のボタンをクリックしてください。
大阪府立東百舌鳥高等学校の稲川孝司先生が「全国高等学校情報教育研究会」で実践報告をされました。
大阪府立東百舌鳥高等学校の稲川孝司先生より,「全国高等学校情報教育研究会」(2014/8/12-13,東洋大学)で実践報告をされました。詳細は詳細はこちら。
「商品開発競争」を公開しました。
新たに,ケーススタディ「商品開発競争」を公開しました。教材のダウンロードには,パスワードが必要です。左記の問い合わせ先まで,mailでお申し込みください。
「交通事故を減らそう」の日本語版をダウンロードできるようにしました。(設定がもれていました。)
「交通事故を減らそう」の日本語版のダウンロードは,こちらからお進みいただき,「ダウンロード」タブをクリックしてください。
BowlandMaths.のDVDをお分けします。
BowlandMaths.の全教材が収められたDVDを,日本の先生方用にと,格安でお分けいただくことができました。定価200ポンドのところを,60%off,送料込みで13,000円でお分けいたします。数に限りがございます。お早めにmailにてお申し込みください。
なお,2014年度中には,すべてのコンテンツがweb上から利用可能になります。
ケーススタディ公開の第二弾は,明治図書「数学教育」の連載(1月号)で紹介予定の「ピザは温かいままで」です。
ケーススタディ公開の第二弾は,明治図書「数学教育」の連載(1月号)で紹介予定の「ピザは温かいままで」です。教材のダウンロードには,パスワードが必要です。左記の問い合わせ先まで,mailでお申し込みください。
科研費報告書をupしました。
ケーススタディ公開の第一弾は,明治図書「数学教育」の連載で紹介した「Outbreak」「クラッシュテスト」です。
webページの改修が完了しました。ボーランドジャパンで開発した教材を紹介する「ボーランド・ジャパンの教材の紹介」を新設しました。また,英国BowlandMaths.の支援により「ケーススタディ」を全面公開できることになりました。順次,公開をしてまいります。
新たな教材の紹介を追加しました。
新着情報は,Bowland JapanのFacebookで行っています。
Bowland JapanのFacebookを立ち上げました
Bowland JapanのFacebookを立ち上げました。また,ボーランドジャパンの掲示板への参加登録も引き続きお待ちしております。
2月18日(土)にBowland Maths.に深く関わっておられる英国の研究者をお招きし講演会を行いました。
2月18日(土)にBowland Maths.に深く関わっておられる英国の研究者をお招きし講演会を行いました。記録はこちらです。
Bowland Japanのメンバーが監修したデジタル教材が,東京都総務局まなぼう統計で公開
Bowland Japanのメンバーが監修したデジタル教材が,東京都総務局まなぼう統計で公開されました。その中にある「やってみよう!統計ミッション」です。
「交通事故を減らそう」(日本語版)の使用とダウンロードはこちら
「交通事故を減らそう」(日本語版)の使用とダウンロードはこちらです。
BowlandMaths.並びにBowlandJapanの活動を報告
2011年12月27日に行われた「第2回科学技術教育フォーラム」において,BowlandMaths.並びにBowlandJapanの活動を報告しました。
2010年に行った「Bowland maths.に関するイングランド実地調査」の報告書
科研費・基盤研究(B)「社会的文脈における数学的判断力の育成に関する総合的研究」の一環として,2010年に行った「Bowland maths.に関するイングランド実地調査」の報告書はこちらです。現地での授業の様子も報告してあります。
1.走り幅跳び
問題
5年生は,来月,体力テストがあります。そのテストの結果をもとに,陸上の選抜チームを作ります。代表の4種目のうち,3種目の代表は決まったのですが,あと一人,はばとびの代表を選ぶ必要があります。
| 1回目 | 2回目 | 3回目 | 4回目 | 5回目 | |
|---|---|---|---|---|---|
| たかし | 355cm | 345cm | 385cm | 360cm | 370cm |
| たける | × | 372cm | 350cm | 390cm | 360cm |
| たけし | 400cm | × | × | 405cm | × |
| たかひろ | × | 385cm | 372cm | × | 378cm |
授業例
概要
体育の学習で行った走り幅跳びの記録から,区連合運動会の代表選手を選出する方法を考える教材で,「他者との相互作用」を促す手立てを講じ,小学校5年生に対して授業を行った。「記録が良い」ことと「失敗が少ない」ことが両立できないような条件を提示したことにより,はじめは一つの視点のみに着目した児童が,他方の意見を聞き,良さを知ることで,結論を変えたり,自分の価値に基づいた判断に自信を深めたり,それぞれの良さを取り入れた折衷案を考えたりする児童がいたことが確認された。一方,他者の考えを理解できずに判断した児童もおり,他者との相互作用を有効に働かせるための手立ての充実が課題として残された。
教材について
本教材は,体育の学習での走り幅跳びの記録を基にして,連合運動会の代表選手を選ぶという,複数の選択肢(4人)の中から,与えられた条件を基にして一つを選びだす問題である。児童は日常の体育の学習で走り幅跳びという種目を行っており,その記録の取り扱いについても理解している。児童は与えられた幅跳びの記録のデータを使用することで選手を選択できることに気づき(A-1定式化),着目した条件に応じて,測定の結果を基に条件を考慮して指標を設定し,場面に応じて推論し(A-3数学的推論・分析),判断の根拠を説明する(A-4解釈・評価,A-5数学的コミュニケーション)という学習活動を行っていく。
選手を選ぶためには,記録だけではなく,ファールを考慮して,自身の価値観をもとに,選手を選ぶ必要がある。また,「学校の代表選手を選ぶ」という設定により,どうしてその選手が幅跳びの代表に選ぶのにふさわしいかを説明する。その際には,どのような考えが基になって選手を選んでいるのかを評価することになる。
2.ソフトボール投げの記録
問題
「ソフトボール投げ」と「走り幅跳び」の種目がある陸上大会に出場する選手を選びたいと思っています。
「かずま君」と「しゅうじ君」の「ソフトボール投げ」と「走り幅跳び」の練習の記録は,次の表のとおりでした。表の「×」印は,ファールとなった場合で,記録がありません。
もし,「かずま君」と「しゅうじ君」のどちらかを選手に選ぶとすると,どちらを選びますか。あなたの考えを説明しなさい。
| 1回目 | 2回目 | 3回目 | 4回目 | 5回目 | |
|---|---|---|---|---|---|
| かずま君 | 21 | 34 | 31 | 19 | 40 |
| しゅうじ君 | 30 | × | × | 34 | 31 |
| 1回目 | 2回目 | 3回目 | 4回目 | 5回目 | |
|---|---|---|---|---|---|
| かずま君 | 3.27 | 2.15 | 3.14 | 3.64 | 2.32 |
| しゅうじ君 | 3.13 | 3.06 | × | 3.25 | × |
3.スポーツテスト
問題
北小学校では,2008年から,児童の体力を伸ばす取り組みを行ってきました。
下の表は,次の5つの種目についての,2007年から2010年の5年生男子の記録の平均値です。
| ソフトボール投げ(m) | 50m走(秒) | 1000m走(分 秒) | 上体起こし(回) | 握力(kg) | |
|---|---|---|---|---|---|
| 2007年 | 27 | 9.0 | 4分8秒 | 20 | 18 |
| 2008年 | 28 | 8.8 | 4分7秒 | 22 | 20 |
| 2009年 | 32 | 9.2 | 4分6秒 | 21 | 21 |
| 2010年 | 34 | 9.1 | 4分10秒 | 23 | 22 |
校長先生は,体力を伸ばす取り組みの成果が表れているのかどうかと悩んでいます。5年生の男子の体力が伸びているといえるか,いえないかを判断しましょう。
4.野球選手のトレード
問題
あるプロ野球チームでは,チームの外野の守備力向上のために,より守備のうまい選手を獲得しようと考えて,二人の選手をリストアップしました。この選手たちの昨年度の成績は以下の表のようになっています。なお,この選手たちは打撃成績,年齢などはほぼ同等です。
| 試合数 | 出場イニング数 | 守備機会 | アウト数 | 刺殺 | 補殺 | 失策 | |
|---|---|---|---|---|---|---|---|
| A | 100 | 750 | 200 | 185 | 180 | 5 | 15 |
| B | 75 | 600 | 150 | 140 | 130 | 10 | 10 |
※出場イニング数…出場した回数(1イニングは3アウトで換算)
守備機会 …その選手の守備範囲に打球が飛んできた回数
刺殺 …外野手の場合,フライを取った回数
補殺 …外野手の場合,おもに返球により走者をアウトにした回数
失策 …その選手の守備範囲にきた打球をエラーした回数
5.先発投手を誰にするか?
問題
草野球のリーグ戦を行っています。若桐ジャガーズは次の試合に負けると,Bクラス入りが決定してしまいます。里田監督は,最も信頼できるピッチャーに次の試合の先発を任せ,このピンチを乗り切りたいと考えています。
あなたが里田監督だったら,どのピッチャーを選びますか。また,選んだ理由についてもいいなさい。
| 投手名 | 勝利数 | 敗北数 | 打者数 | 投球回数 | 被安打 | 被本塁打 | 与四球 | 奪三振 | 失点 | |
|---|---|---|---|---|---|---|---|---|---|---|
| A | 寺崎 | 12 | 10 | 705 | 170 | 162 | 4 | 43 | 112 | 67 |
| B | 塩津 | 14 | 8 | 699 | 177 | 148 | 13 | 31 | 150 | 57 |
| C | 高田 | 9 | 9 | 638 | 154 | 144 | 7 | 34 | 113 | 42 |
6.バスケの強化選手を選抜しよう
問題
武田中学校のバスケットボール部は,部員数8名で活動している。次の大会に向けて,監督は8名のうち,試合に出る5名を選出し,残りの3名を控え選手としなければならない。下の表は,各選手の身長,最近1ヶ月の練習試合でその選手が決めた得点の合計,および,監督による評価(※1)をまとめたものである。
※1 監督による評価とは,監督がふだんの練習や練習試合等をみて,いくつかの観点について各選手を評価し,A(優れている),B(ふつう),C(努力が必要)という3段階で記入したものである。
選手を選んだ理由については,後日,選手の保護者の前で説明しなければならない。そこで,監督は下の表にもとづいて選手を選ぶことにした。[2] [3] [6]の3名を選んだところで,あと2名を誰にするか決めかねている。あなたが監督であるとして,選手 [1] ~ [8] のうち,どの2名を選手にするか [1] ~ [8] の記号で答えなさい。また,その2名の選手を選んだ理由について,保護者の前でどのように説明するか,実際に説明しなさい。
| 選手 | 身長 | 得点 | スピード | スタミナ | シュートの うまさ |
ディフェンス(守り)の うまさ |
ミスの 少なさ |
部活動の 出席率 |
|---|---|---|---|---|---|---|---|---|
| [1] | 175 | 4 | C | B | B | B | A | A |
| [2] | 172 | 10 | A | B | B | A | B | A |
| [3] | 164 | 18 | B | B | A | B | A | A |
| [4] | 161 | 8 | C | A | C | A | B | A |
| [5] | 156 | 20 | A | A | A | C | B | C |
| [6] | 150 | 24 | A | B | A | A | A | B |
| [7] | 146 | 8 | A | B | C | A | A | A |
| [8] | 138 | 14 | A | C | A | B | B | B |
授業例
概要
本稿は,「バスケットボールの選手を選ぼう」という問題を教材化し,実践した授業の報告である。中学校の部活動(バスケットボール部)に所属する8名の選手の中から,試合に出る5名の選手を監督の立場に立って選ぶ場面を設定した。さらに,それらの選手を選んだ理由について,選手の保護者に説明するという場面を設定することで,より公平・公正な考えが求められるようにした。実際の授業においては,公平・公正な選出を考え,数値化するアイデアが出たり,生徒の発言や記述の中に,どのような方針で判断したのかによって,結論が異なるということに言及している事実が明らかとなった。
教材について
この教材は,運動部に所属する生徒にとっては切実な問題である。中学生は選手を選ぶという立場に立つ機会は少ない。しかし,生徒同士の会話の中で,好きなプロスポーツチームの先発選手を予想したり,日本代表チームの選手選考について,予想したり,妥当性を議論したりする経験は少なくない。以上のことから,本問題に対する生徒の関心は高いことが予想される。
バスケットボールに限らず,スポーツにおいて選手を選考する根拠となる要素は多岐にわたり,どの要素を判断材料とするかは難しい問題である。さらに,1つ1つの要素に対する評価の妥当性も問われよう。そこには,選手を選考する側の人間が,どのような方針(価値観)をもっているのかが大きく関わってくる。例えば,バスケットボールでは,シュートやパスのうまさやスピード,ジャンプ力,スタミナなどは大切である。しかし,どんなに技術があっても,ミスのない安定したプレイができるかという視点も重要である。また,ここぞというときの勝負強さ(メンタル面)も重要視されている。
スピードという要素1つをとってみても,直線を走る速さだけでなく,細かく方向転換できる俊敏性も重要となる。20mを速く走ることも大切であるが,短い距離ではやく加速する瞬発力も問われるなど,1つの要素に求められることは多岐にわたる。
このように,生徒の関心は高い題材ではあるものの,判断の根拠となる要素について,どのように扱うかという部分については,生徒にとって困難性がある題材である。そこで,いくつかの意図的な場面設定をすることで,生徒に考えやすい課題となるように工夫した。
第1に,保護者の前で説明するという場面の設定である。このことにより,公平・公正な考えが求められるようになる。先にも触れたように,この課題は生徒たちが自分の方針を押し通してしまい,自分の判断の妥当性を問わない(数学を使おうとしない)ことも考えられる。保護者の前で説明するという条件に合わせ,公平・公正に判断しようとすれば,数値化するアイデアに結びつくことも予想される。すべての要素を数値化したり,いくつかの要素に限定して数値化したり,さまざまな方法で数学化することが期待できよう。
第2に,判断材料となるデータを身長,得点,監督による3段階評価に限定したことである。バスケットボールという競技自体をどの程度知っているかによって,問題の取り組みやすさは変わってくる。したがって,保健体育科での指導内容やスポーツ全体に共通しているような要素に限定することで,より多くの生徒にとって実感のあるデータとした。例えば,監督による評価には,イメージしやすいもののみとした。「部活動の出席率」は生徒の選手選出における方針(価値観)に揺さぶりをかけることがねらいである。技術面を重視するか,取り組み面を重視するか,中学生にとって対立や葛藤が起きやすい部分である。対立や葛藤によって議論が白熱し深まるのではないかと期待し,「部活動の出席率」という項目を設定した。
例えば,得点やスピード,スタミナ,シュートのうまさのある[5]を選んだ生徒に対して,出席率がCであることをあげて,「技術面だけを重視したのではすべての保護者が納得しないのではないか」という議論が起こることが期待される。それに対し,「部の方針として技術面を重視することをきちんと説明すればよい」(判断の基準(方針・価値観)が何だったのか)や「出席率は今後の指導で改善していくことも説明すればよい」(仮定が変われば結論がどう変わるか)など,方針(価値観)についての議論が白熱するであろう。
第3に,問題の単純化である。例えば,3名はすでに決定しており,残りの2名を選出するとしたこと,監督による評価を3段階評価にしたことなどである。実際にはこれらの項目がどのようにして3段階評価されたかという基準も問題となるところであるが,ここまでの部分については,問題の仮定として設定することとした。
第4に,条件設定の工夫である。すでに選ばれている3名には,評価でCを入れないこととし,長所がバランスよく配置されるように工夫をした。選考対象となる残りの5人については,短所のバランスも配慮した。
7.アーリーランチコンクール
問題
南中学校では,給食を早く食べ始められるようにするために「ランチ・コンクール」を行っています。1学期は,給食を食べ始めた時刻を調べ,優勝クラスを決めました。
生活委員会では,来週,2学期の「ランチ・コンクール」を行うことにしました。その際,1学期とは異なる決め方で優勝クラスと準優勝クラスを決めることにしました。そして,給食を食べ始めた時刻だけでなく,4時間目が移動や着替きがえに時間が必要な体育になっている曜日と,給食時間中のマナーの向上に目を向けるために給食時間中に立ち歩いた人数を調べることにしました。
下の表は,各クラスの生活委員が,一週間,記録した結果です。例えば,1組の月曜日に記録されている「12:55」は,給食を食べ始めた時刻を表し,「2」は,給食時間中に立ち歩いた人数を表しています。また,表の中の ●は4時間目が体育の日を表しています。あなたは何組を優勝にしますか。また,準優勝は何組にしますか。
| 1組 | 2組 | 3組 | 4組 | 5組 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 月 | 12:55 | 2 | 12:54 | 0 | 13:06 | 2 | ●12:48 | 3 | 12:55 | 0 |
| 火 | 12:58 | 1 | ●13:03 | 1 | 12:52 | 3 | 13:02 | 2 | 12:50 | 2 |
| 水 | 12:50 | 1 | 12:58 | 0 | 12:50 | 0 | 12:51 | 3 | 13:01 | 1 |
| 木 | 13:02 | 2 | 12:52 | 0 | 12:48 | 2 | 12:55 | 0 | 12:56 | 0 |
| 金 | ●12:51 | 0 | ●13:00 | 1 | 12:49 | 4 | 12:54 | 2 | 12:58 | 1 |
8.美化コンクール
問題
ある中学校で美化コンクールが行われました。結果は次の表のようになっています。優勝,準優勝はどのクラスにするとよいでしょうか。
| 1組 | 2組 | 3組 | 4組 | 5組 | |
|---|---|---|---|---|---|
| 黒板 | ◎ | △ | ◎ | ◎ | △ |
| 黒板のさん | △ | △ | × | △ | △ |
| 掃除用具入れの中 | × | × | ◎ | △ | △ |
| ロッカーの上と中 | 〇 | ◎ | ◎ | × | △ |
| 机の並び | △ | 〇 | × | ◎ | △ |
9.体育祭の優勝クラスは?
問題
【 ver.1 】
ある中学校で体育祭の予行練習が行われました。各種目の順位は以下の表の通りで,1位には50点,2位は45点,3位は40点,4位は35点,5位は30点(失格は0点)が入ります。
| 1組 | 2組 | 3組 | 4組 | 5組 | |
|---|---|---|---|---|---|
| 100m走 | 1 | 3 | 4 | 2 | 5 |
| 全員リレー | 2 | 失格 | 4 | 3 | 1 |
| ムカデ競走 | 5 | 3 | 4 | 1 | 2 |
| 縄跳びリレー | 5 | 2 | 4 | 1 | 3 |
| 選抜リレー | 1 | 2 | 3 | 失格 | 4 |
予行練習が終わった後で,「1組はクラス全員で協力する種目であるムカデ競走や縄跳びリレーが最下位なのに,優勝するなんて,変だなあ。1組はただ足が速い人が多いだけじゃないか。」「4組はクラスで団結する種目(ムカデや縄跳び)が1位だったのに,準優勝もできないなんて,おかしいなあ」という意見がありました。
そこで,体育祭本番に向けて各種目で配点を変えて,協力できるクラス,団結力があるクラスが優勝できるようにしたいと考えました。どのような配点にすればいいですか。またその時の,優勝クラス,準優勝クラスはどこになりますか。
各種目の出場人数や,練習時間の目安は以下の通りです。
| 出場人数 | 練習時間の目安 | |
|---|---|---|
| 100m走 | 4人 | 朝練(個人練習) |
| 全員リレー | クラス全員(38人) | 放課後練習2日間 |
| ムカデ競走 | クラス全員(38人) | 放課後練習10日間 |
| 縄跳びリレー | 3人×5組 | 朝練 |
| 選抜リレー | 4人 | 朝練 |
※ 朝練は自由参加で7:30 ~ 8:10 放課後練習はクラス全員参加で1時間
(開発者:関)
【 ver.2 】
ある中学校では,学園祭の体育部門として,4クラス対抗で6つの種目を行っている。目的は,クラスで協力して行う種目で,互いに競い合うことを通して,クラスの団結をはかり,他クラスとの交流を深めることである。それぞれの種目で順位をつけて1位が50点,2位が30点,3位が20点,4位が10点というように得点をつけていく。最終的に,6種目の合計得点で総合優勝を争う。下の表は今年の結果である。
| 種目 | 1組 | 2組 | 3組 | 4組 | |
|---|---|---|---|---|---|
| 1 | 大なわとび | 50(112回) | 30(78回) | 10(66回) | 20(70回) |
| 2 | 障害物リレー | 30(5分32秒) | 50(5分02秒) | 20(5分34秒) | 10(5分40秒) |
| 3 | 玉入れ | 30(56個) | 20(45個) | 50(72個) | 10(43個) |
| 4 | つなひき | 20(3位) | 10(4位) | 30(2位) | 50(1位) |
| 5 | ムカデ競走 | 20(1分56秒) | 30(1分41秒) | 10(3分42秒) | 50(1分34秒) |
| 6 | 全員リレー | 20(11分02秒) | 10(11分02秒) | 50(10分12秒) | 30(10分40秒) |
| 合計得点 | 170 | 150 | 170 | 170 |
※ 表の数値は,各種目の得点であり,( )内は各種目の記録である。
全種目が終了したが,3クラスが同点優勝となった。賞状は3クラスに出すことにしたが,優勝カップは1つしかない。そこで,種目ごとの記録をもとにもっとも成績が良いクラスに優勝カップを渡すことになった。どのクラスがふさわしいといえるだろうか。(開発者:櫻井)
10.日帰り温泉
問題
おさむさんは練馬区に住んでいます。休日,家族みんなで日帰り温泉に行くことになりました。練馬インターチェンジから関越自動車道にのって行く日帰り温泉旅行のプランを立てるようにとお父さんから言われました。おさむさんは,家族みんなが満足できるような旅行にしたいと思いました。
総合的に判断すると,どの温泉施設をおさむさんに勧めますか。
おさむさんの家族
- 父 会社員
車を運転するのが好きだからなるべく遠くに行きたいな。 - 母 小学校の先生
出費が心配,でもどうせ行くならなるべく人気のある温泉に行きたいわ。 - おさむさん 中学2年生
正直言うと,家族と温泉に行くよりも友達とサッカーをするほうがいいんだけど。
でも,どうせ行くなら温泉施設でなるべく長い時間を過ごしたいな。 - 妹 小学5年生
いろいろなお風呂のある温泉に行きたいな。
| インター チェンジ名 |
練馬からの 時間(分) |
高速料金 (円)片道 |
入浴料(円) | 施設の特徴 | 人気ラン キング(位) |
|
|---|---|---|---|---|---|---|
| おとな | 子ども (小学生まで) |
|||||
| 所沢 | 13 | 250 | 1950 | 1050 | 市街地に立地。プールも楽しめる。 | 6 |
| 川越 | 25 | 400 | 850 | 400 | 川越インターの近くに立地。 9種類のお風呂と3種類のサウナが楽しめる。 |
5 |
| 嵐山小川 | 44 | 800 | 1280 | 640 | 大浴場や露天風呂など多彩なお風呂を楽しむことができる。 | 3 |
| 花園 | 50 | 900 | 1030 | 1030 | 都心から少し離れた場所、静かに広がる田園風景に立地。 天然の露天風呂をはじめ様々な温泉がある。 |
1 |
| 本庄児玉 | 72 | 1100 | 700 | 400 | 都心から少し離れた場所、静かに広がる田園風景に立地。 天然の露天風呂をはじめ様々な温泉がある。 |
7 |
| 前橋 | 80 | 1400 | 500 | 300 | 見晴らしのよい露天風呂と広々とした大浴場が楽しめる。 | 2 |
| 渋川伊香保 | 89 | 1500 | 600 | 300 | 群馬・長野県境部に立地。総檜造りの大浴場と、森に面した露天岩風呂。 | 4 |
11.A社とB社の電池の稼働時間
問題
電池を作っている電器メーカーのA社とB社は,来週行われる大きな取引のライバル会社です。もしここで取引が決まれば売り上げがかなり伸びで,どちらの会社でも準備に大忙しです。A社の電池とB社の電池は値段がほぼ同じなので,特に決め手にはなりません。
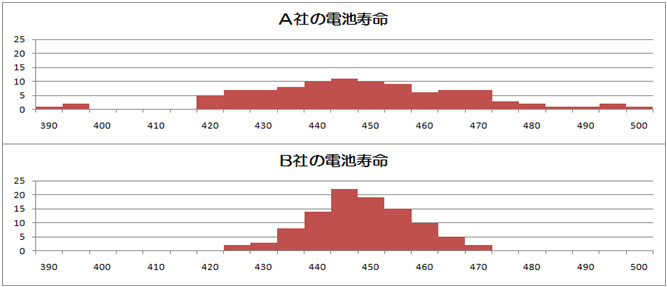
そこで,A社とB社の電池100個ずつの稼働時間(電池寿命)についてまとめた次のデータを元に,どちらの会社も性能の良さで売り込むことに決めました。
| A社 | B社 | |
|---|---|---|
| 平均 | 447.9 | 448.1 |
| 最頻値 | 445 | 445 |
| 中央値 | 447 | 448 |
| 最小値 | 391 | 423 |
| 最大値 | 501 | 472 |
| 範囲 | 110 | 49 |
(5時間ごとの度数をまとめたヒストグラム) (※例えば440の階級には,437.5~442.5 のデータが入っています)
(1)A社はどのように売り込めばいいと思いますか。
(2)B社はどのように売り込めばいいと思いますか。
12.ガソリンの割引カード
問題
 下図のように道路をはさんで,2つのガソリンスタンド店がある。昨日までA店,B店ともに140 円/リットルでガソリンを販売していたがA店は120 円/リットルに値下げをした.そこで,B店はガソリン割引カードをお客に配布して使ってもらうことにした。
下図のように道路をはさんで,2つのガソリンスタンド店がある。昨日までA店,B店ともに140 円/リットルでガソリンを販売していたがA店は120 円/リットルに値下げをした.そこで,B店はガソリン割引カードをお客に配布して使ってもらうことにした。
 Chance!とある③ ⑥ ⑨ ⑫の3回目,6回目,9回目,12回目の給油でガソリンの値段の割引が行われる。また,このカードは1回につき20リットル以上給油しなければ,このカードは使えない。また,このガソリン割引カードの値引きは,3回目と6回目の給油のときが2円引き,9回目が3円引き,12回目が5円引きである。
Chance!とある③ ⑥ ⑨ ⑫の3回目,6回目,9回目,12回目の給油でガソリンの値段の割引が行われる。また,このカードは1回につき20リットル以上給油しなければ,このカードは使えない。また,このガソリン割引カードの値引きは,3回目と6回目の給油のときが2円引き,9回目が3円引き,12回目が5円引きである。
A店とB店では,どちらが安く給油できるだろうか。
13.モノレールの料金比較
問題
たつやさんは,「多摩都市モノレール」をいつも利用しています。多摩都市モノレールより後に開業した,「舎人(とねり)ライナー」の運賃表を見たたつやさんは,多摩都市モノレールより料金が安いと感じました。そこで,「多摩都市モノレール」の運賃の値下げを求める提案をしようと考えました。
あなたはたつやさんの同級生です。説得力のある提案になるように,たつやさんに具体的にアドバイスしましょう。
| 駅前 | 営業キロ(km) | 運賃(円) |
|---|---|---|
| 上北台 | 0 | / |
| 桜街道 | 0.7 | 100 |
| 玉川上水 | 1.5 | 200 |
| 砂川七番 | 2.5 | 200 |
| 泉体育館 | 3.0 | 200 |
| 立飛 | 3.6 | 250 |
| 高松 | 4.2 | 250 |
| 立川北 | 5.4 | 300 |
| 立川南 | 5.8 | 300 |
| 柴崎体育館 | 6.5 | 300 |
| 甲州街道 | 8.0 | 350 |
| 万願寺 | 9.3 | 350 |
| 高幡不動 | 10.5 | 400 |
| 程久保 | 11.3 | 400 |
| 駅前 | 営業キロ(km) | 運賃(円) |
|---|---|---|
| 日暮里 | 0 | / |
| 西日暮里 | 0.7 | 160 |
| 赤土小学校前 | 1.7 | 160 |
| 熊野前 | 2.4 | 220 |
| 足立小台 | 3.0 | 220 |
| 扇大橋 | 4.1 | 270 |
| 高野 | 4.6 | 270 |
| 江北 | 5.2 | 270 |
| 西新井大師西 | 6.0 | 270 |
| 谷在家 | 6.8 | 270 |
| 舎人公園 | 7.7 | 320 |
| 舎人 | 8.7 | 320 |
| 見沼代親水公園 | 9.7 | 320 |
14.どの会社に就職するか
問題
4つの会社が,次のような社員広告を出しています。
| (A社) | アルバイト募集 | 時給 910円 |
| (B社) | アルバイト募集 | 日給 7,300円 |
| (C社) | 正社員募集 | 月給 12万円,ボーナス 2か月分 昇給 年1回 月額 3,000円 |
| (D社) | 正社員募集 | 月給 10万円,ボーナス 3か月分 昇給 2年に1回 月額 10,000 円 |
どの会社の場合も,1日に働く時間や1か月に働く日数について,いろいろと相談することができます。あなたなら,どの会社への就職を希望しますか。その理由も説明しなさい。
15.バレーボールの勝敗
問題
6人制のバレーボールの試合は,2つのチームが4 セットの試合を行い,先に3セットをとったチームが勝ちとなります。ただし,両方のチームが2セットをとった場合は,5セット目を行います。それぞれのセットは,25 点ですが,5セット目だけは15 点になっています。(セットの勝敗は,先に25 点か15 点をとったチムが勝ちとなりますが,同点の場合は,連続して2点をとる必要があります。)
次に示す新聞記事は,2010 年(平成22 年)12 月19 日に行われた全日本選手権の準決勝の結果を示したものです。男子は,「JT」と「サントリー」が,女子は「デンソー」と「東レ」が決勝に進んだことがわかります。(略)
ところで,スポーツの中には,勝敗を決めるときに,バレーボールのように,いくつのセットをとったかで勝敗が決まるものと,野球やサッカーのように,得点の合計で勝敗が決まるものがあります。
新聞記事の試合で,おしくも敗れてしまったチームに対して,次のような“はげましの言葉”をおくったとします。
「試合には勝てなかったけれど,得点の合計では,みなさんの方が多くの点をとったのだから,みなさんの方が実力は上ですよ!」このはげましの言葉について,あなたはどのように考えますか?
16.伝統技術展の見学への移動方法を決めよう
問題
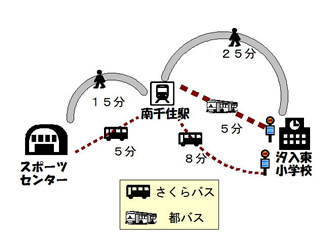
4年生全員で,伝統技術展の見学へ行きます。どうやって行けばいいのでしょう。
| 日時 | 7月 |
| 場所 | 荒川スポーツセンター |
| 人数 | 4年生 106人 |
| 都バス | 70人乗り(うち座席 25名分) |
| さくらバス | 30人乗り(うち座席 15名分) |
| ※ 学校割引で料金はどちらも同じ | |
授業例
概要
学校から校外学習先までの行き方のプランを考える教材で,数学的判断力の育成を目指し,小学校4年生に対して授業を行った。その結果をプロセス能力の水準を視点に分析したところ,問題に対して自分なりの価値観をもって判断し,与えられた問題を解決する児童がいたことが確認された。一方,根拠をもって自分の考えの妥当性を述べること,また,他者の別のアプローチによる判断結果と自身の判断結果を対比して評価することに関する課題が明らかになった。
教材について
この教材は,児童の在籍校である汐入東小学校から,伝統技術展の会場であるスポーツセンターまでの行き方のプランを下級生のために立てるものである。児童は7月に実際に「伝統技術展」へ行っており,自身の経験を活かせる本題材は,児童にとって取り組みやすい題材である。
プランを作成するには,人数,時間,時刻を考慮して,自身の価値観をもとに,交通手段を選ぶ必要がある。また,「先生に伝える」という設定により,自分の作成したルートプランに合うキャッチフレーズを付け,説明する。その際には,キャッチフレーズとの整合性を評価することになる。
17.修学旅行のルートを決定しよう
問題
《 来年の修学旅行計画書 》
来年の大宮東中学校の修学旅行3日目は,班ごとに半日タクシーで京都市内にある世界文化遺産に登録されている17の有名な寺社等を,なるべくたくさん見学することにしました。そこで,多くの生徒が見学すると考えられる7 所を選びました。なお,宿泊する旅館は,南禅寺から徒歩3分の所にある旅館なので,出発地点は南禅寺にします。到着地点は,新幹線に乗るために京都駅とします。
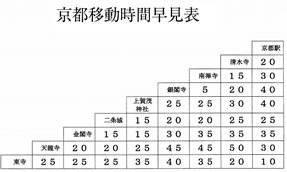 修学旅行計画書に示したように,タクシーを使って半日でなるべくたくさんの世界文化遺産を見学することにしました。 見学しようと選んだ場所は,【金閣寺】【天龍寺】【清水寺】【銀閣寺】【二条城】【東寺】【上賀茂神社】の7ヵ所で,出発地は南禅寺,到着地は京都駅です。
修学旅行計画書に示したように,タクシーを使って半日でなるべくたくさんの世界文化遺産を見学することにしました。 見学しようと選んだ場所は,【金閣寺】【天龍寺】【清水寺】【銀閣寺】【二条城】【東寺】【上賀茂神社】の7ヵ所で,出発地は南禅寺,到着地は京都駅です。
(1) 来年の修学旅行に行く後輩のために見学ルートのプランをつくってください。
(2)7ヵ所全てを見学するルートは,つくれないことがわかりました。それでは,来年の後輩のために,改めて見学プランをつくってください。
授業例
概要
中学校3年で実施される修学旅行の見学ルートプランを考える教材を開発し,数学的・社会的価値認識による判断力をはぐくむことを目的として,中学3年生に対して授業を行った。その結果,事象を「点」で,関係を「線」で図形的(図的)にとらえ,事象間の複雑な関係を図を用いて課題を解決することができた。課題の構造を図形化(図的)することで簡潔に考えていく数学的な考え方の素晴らしさを生徒に感じさせ,生徒の解決過程や授業感想より数学的・社会的価値認識から社会的価値による判断力をはぐくむことができたと考える。
教材について
7ヵ所の世界文化遺産および出発地の南禅寺,到着地の京都駅は,図1の京都散策マップより,それぞれの場所を確認することができる。しかし,図1の地図では,【課題】を解決することはできない。そこで定式化を行う。
18.どの電車を使うかな
問題
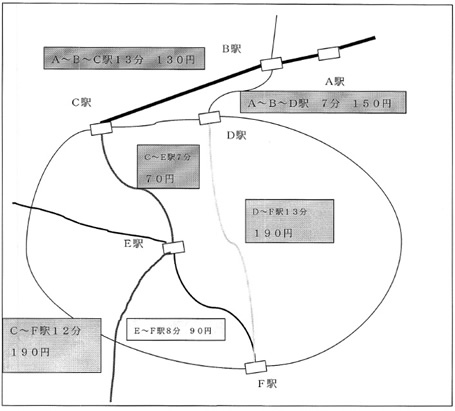 あきらさんの家族は,日曜日に,A駅から電車に乗って,F駅まで行き,F駅の近くにある遊園地に遊びに行きます。どの線を通っていけばよいでしょか。
あきらさんの家族は,日曜日に,A駅から電車に乗って,F駅まで行き,F駅の近くにある遊園地に遊びに行きます。どの線を通っていけばよいでしょか。
ただし,乗り換えをするときには5分かかります。また,同じ太さの線や同じ色の線は,同じ路線(電車)を表しています。
19.24時間列車の旅
問題
2011年(平成23年)9月24日の北海道新聞(朝刊)の記事である。「24時間以内に列車で移動できる距離の記録」における新記録達成を報じたもので,ギネスブックへの申請についても触れている。
「東京のトラベルライター白川淳氏(47)が,9月22日に北海道の稚内駅から鹿児島県の鹿児島中央駅まで,23時間57分かけて3072.4㎞を移動した。当初は3月11日に出発する予定であったが,東日本大震災のため,東北新幹線のダイヤの完全復旧(9月23日)を踏まえて9月22日に出発した。稚内駅から鹿児島中央駅まで,7本の列車を乗り継いで新記録を達成したが,この試みは従来も,新幹線網が発達し列車の運行が正確な日本で生まれてきている。これまでの記録は,2009年11月に日本在住のアメリカ人が,北海道の天塩中川から鹿児島中央駅までの2969.5kmだった。」
(1) これを達成するには,どのようなことを考えなければならないか。
(2) 3月11日の出発を断念したのはなぜか。
(3) 東北新幹線の復旧(9月23日)の前日(9月22日)に稚内を出発したのはなぜか。
(4) 2009年の記録とは何が違うのか,また,何が同じか。
(5) 同様なこと(24時間で移動すること)で,新たな記録は作れないか。列車に限定せず,飛行機や船なども使って24時間で,どれくらい移動できるか。